Detecting Arbitrage in Trading Using Graph Theory

Negative weight edges can create negative weight cycles i.e. a cycle that will reduce the total path distance by coming back to the same point.

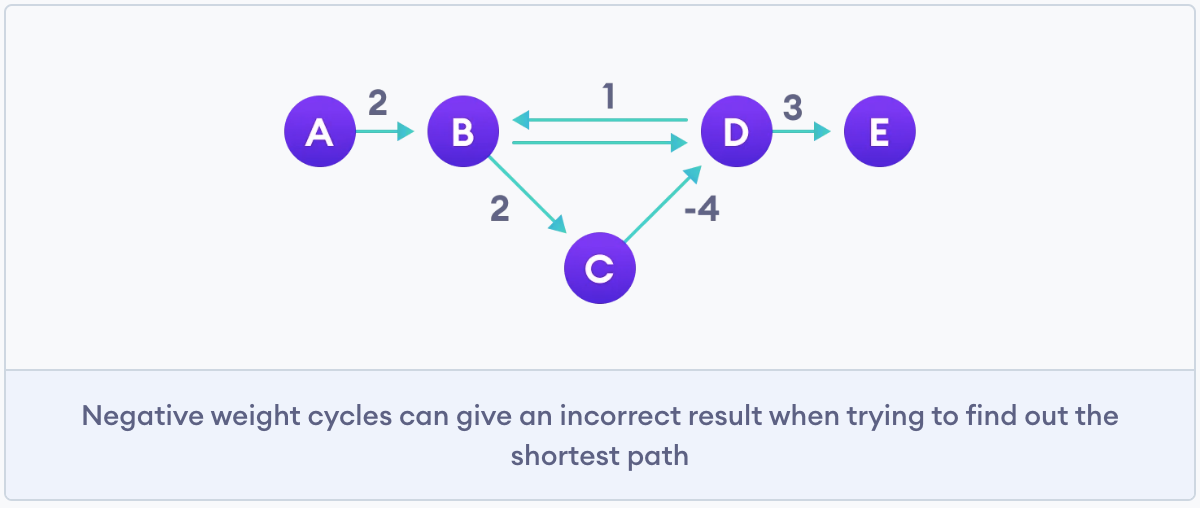
Shortest path algorithms like Dijkstra's Algorithm that aren't able to detect such a cycle can give an incorrect result because they can go through a negative weight cycle and reduce the path length.

Bellman Ford algorithm works by overestimating the length of the path from the starting vertex to all other vertices. Then it iteratively relaxes those estimates by finding new paths that are shorter than the previously overestimated paths. By doing this repeatedly for all vertices, we can guarantee that the result is optimized.

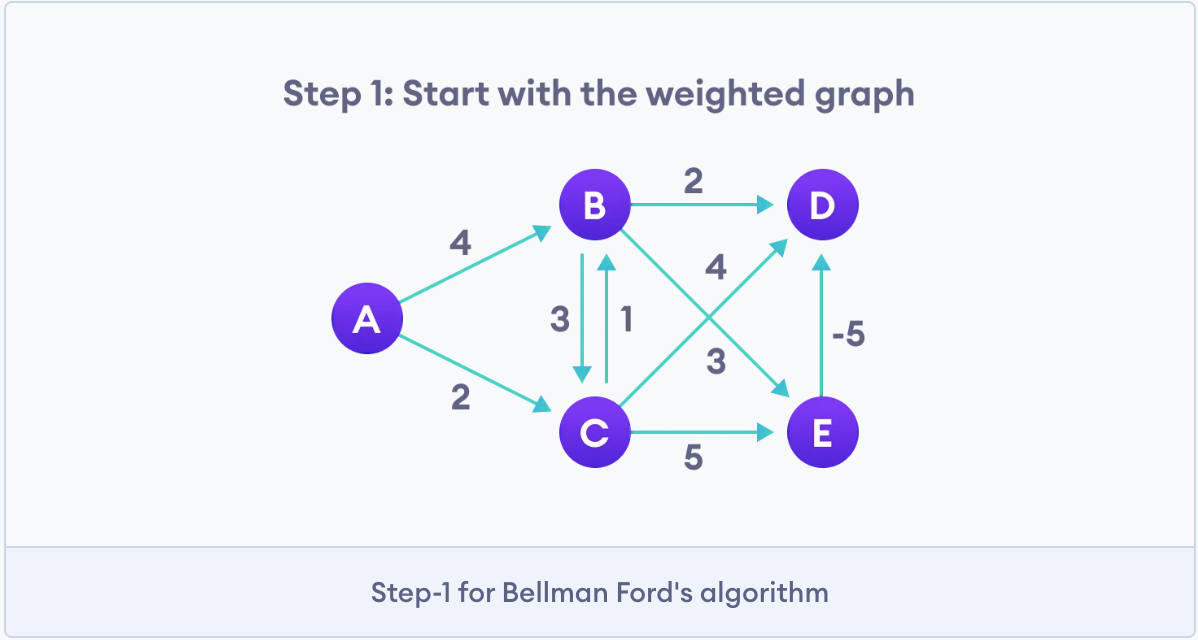
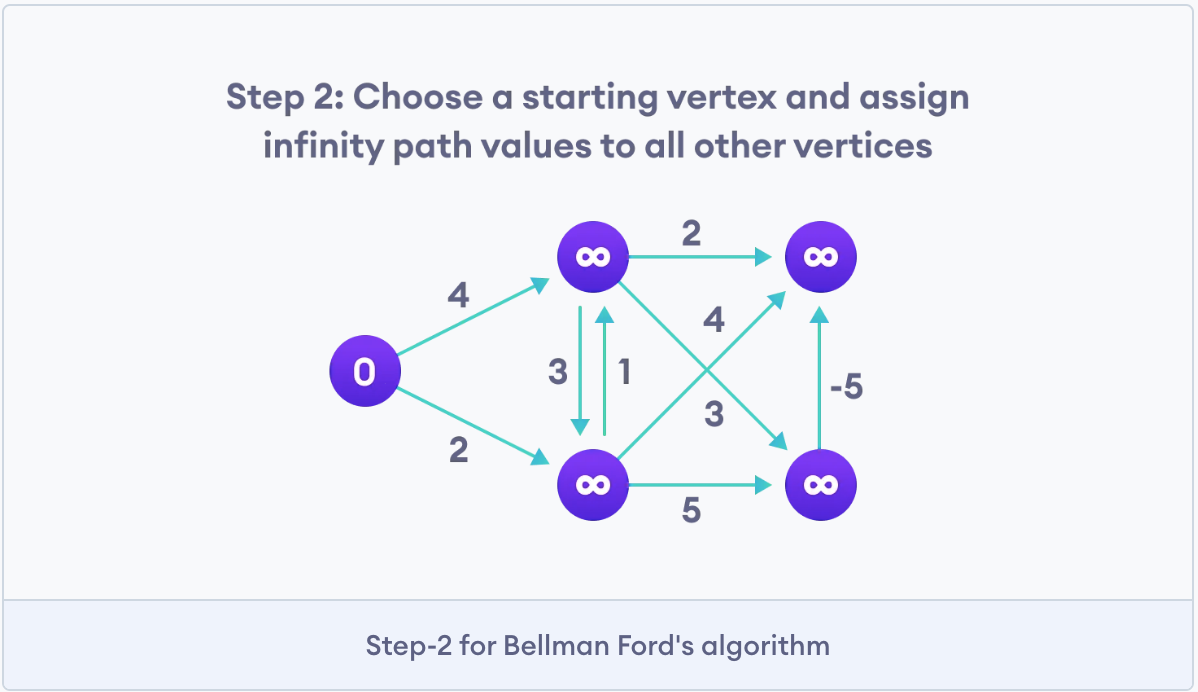
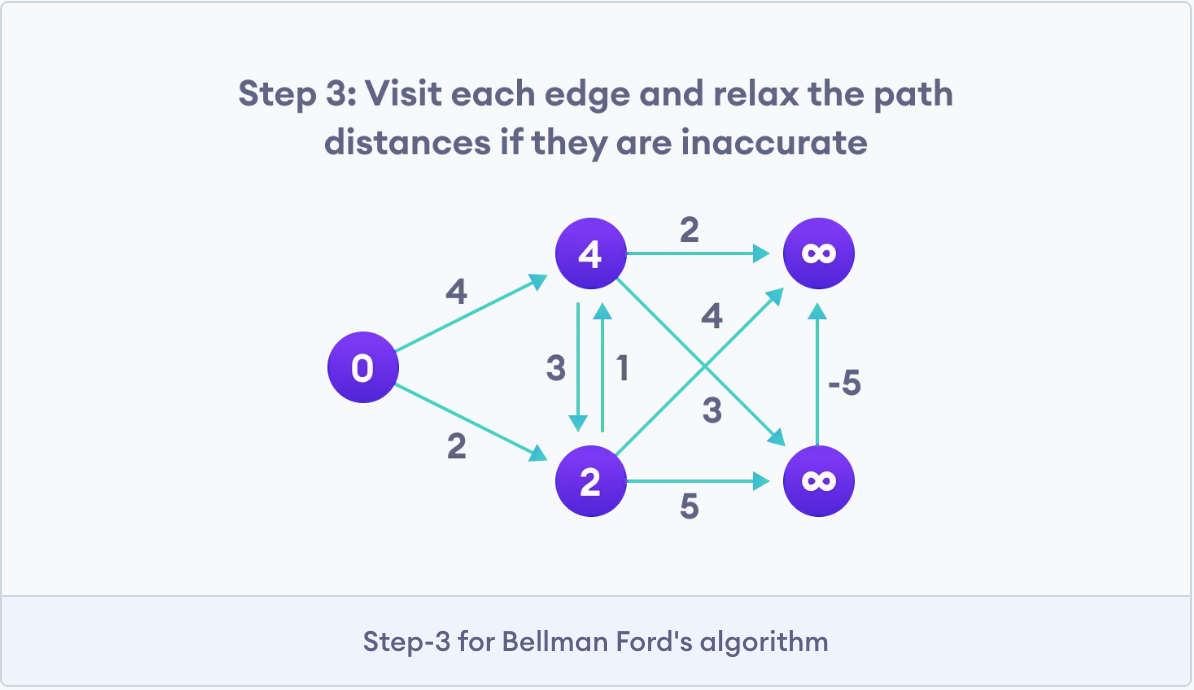
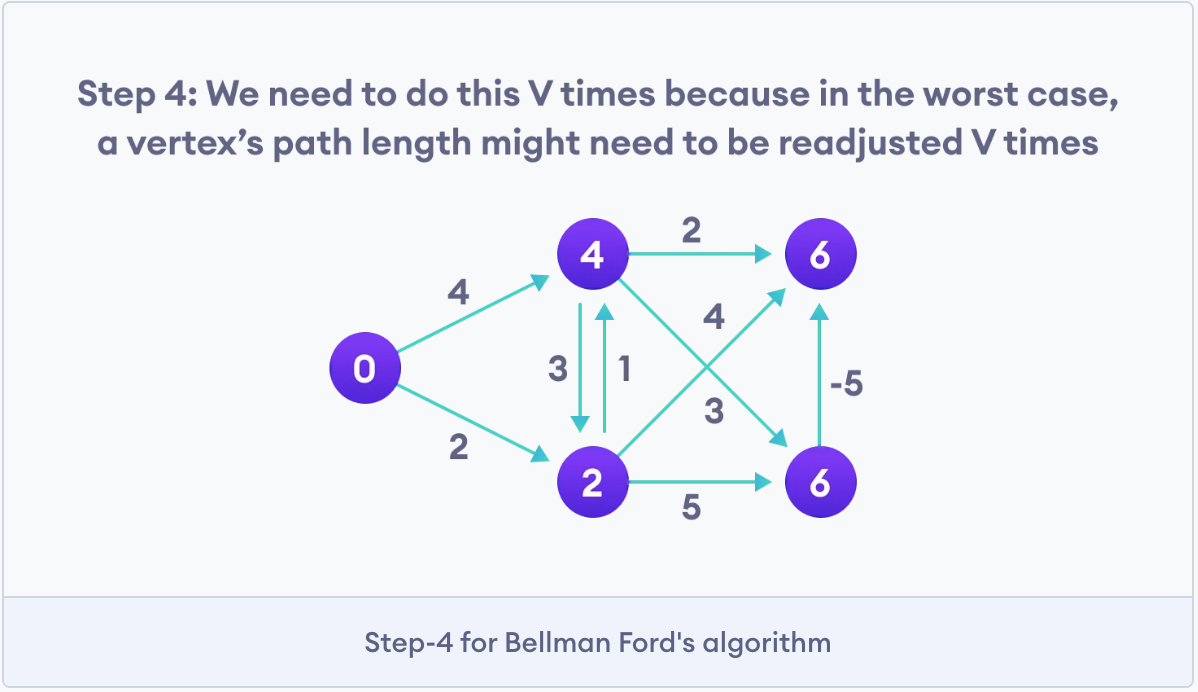
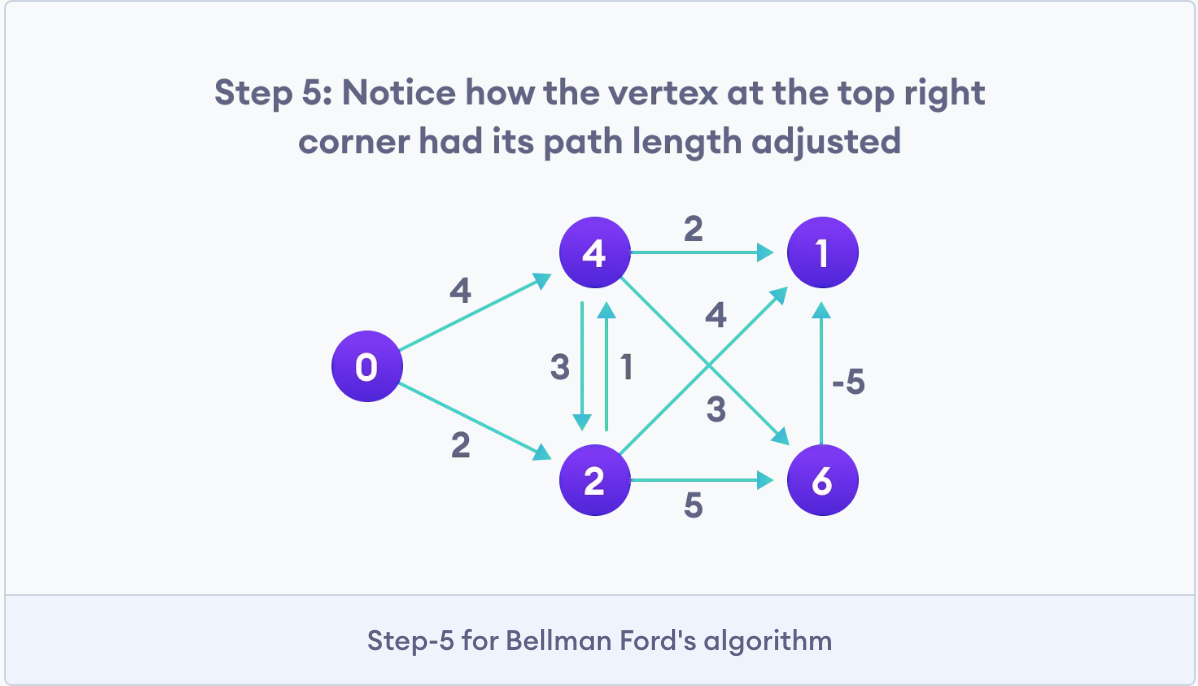
Photo credit goes to programiz.com

Step 1: Define the Graph Structure

type Edge struct {
	from, to int
	weight   float64
}

type Graph struct {
	vertices int
	edges    []Edge
}

// NewGraph creates a new graph with a specified number of vertices
func NewGraph(vertices int) *Graph {
	return &Graph{vertices: vertices, edges: []Edge{}}
}

// AddEdge adds a directed edge with a weight (negative log of the rate) between two vertices
func (g *Graph) AddEdge(from, to int, rate float64) {
	weight := -math.Log(rate)
	g.edges = append(g.edges, Edge{from: from, to: to, weight: weight})
}

Step 2: Implement Bellman-Ford Algorithm

// DetectArbitrage uses the Bellman-Ford algorithm to detect negative weight cycles, which indicate arbitrage opportunities in trading.
func (g *Graph) DetectArbitrage(src int) bool {
	// Step 1: Initialize distances from the source to all other vertices as infinity, except the source itself.
	// This represents the initial assumption that all other currencies are infinitely far from the source currency.
	distances := make([]float64, g.vertices)
	for i := range distances {
		distances[i] = math.Inf(1)
	}
	distances[src] = 0

	// Step 2: Relax edges repeatedly.
	// Relaxing an edge means trying to improve the shortest known distance to a vertex by using an edge from another vertex.
	// If a shorter path is found, the distance to the vertex is updated.
	for i := 1; i < g.vertices; i++ {
		for _, edge := range g.edges {
			if distances[edge.from] != math.Inf(1) && distances[edge.from]+edge.weight < distances[edge.to] {
				distances[edge.to] = distances[edge.from] + edge.weight
			}
		}
	}

	// Step 3: Check for negative weight cycles.
	// After relaxing all edges, we do one more pass over all edges to see if we can still find a shorter path.
	// If we can, it means there is a negative weight cycle in the graph, indicating an arbitrage opportunity.
	for _, edge := range g.edges {
		if distances[edge.from] != math.Inf(1) && distances[edge.from]+edge.weight < distances[edge.to] {
			return true // Negative cycle detected, indicating an arbitrage opportunity
		}
	}

	// No negative cycles detected, hence no arbitrage opportunities.
	return false

Step 3: Example Usage

func main() {
	// A new graph is created with 4 vertices. Each vertex represents a different currency.
	graph := graph.NewGraph(4)

	// Representing exchange rates with negative logarithms. Exchange rates are converted to
	// negative logarithms to transform the problem into the shortest path problem.
	graph.AddEdge(0, 1, 0.5)  // USD to EUR
	graph.AddEdge(1, 2, 2.0)  // EUR to GBP
	graph.AddEdge(2, 3, 1.5)  // GBP to JPY
	graph.AddEdge(3, 0, 0.75) // JPY to USD

	// The method is called with source vertex 0, representing the starting currency (USD in this case).
	// currencyIndex: [USD": 0,"EUR": 1, "GBP": 2, "JPY": 3]
	if graph.DetectArbitrage(0) {
		slog.Info("Arbitrage opportunity detected!")
	} else {
		slog.Info("No arbitrage opportunity found.")
	}
}

For the full code, please visit gitHub repository, Trading Arbitrage Detector